陕西宝鸡市陈仓区等2地2022-2023学年高三下学期三模数学（理）试题(含参考答案)

2023届高三第十二次模考数学（理科）试卷 第I卷选择题（共60分） 本试卷共4页，23题（含选考题）.全卷满分150分.考试用时120分钟. 一 ､选择题 ：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.请将正确的答案填涂在答题卡上.） 1.设 ，则 （ ） A. B. C.1 D.-1 2.设集合 .若 ，则 （ ） A.-3 B.-1 C.1 D.3 3.某中学高一 ､高二和高三各年级人数见下表 .采用分层抽样的方法调查学生的健康状况，在抽取的样本中，高二年级有20人，那么该样本中高三年级的人数为（ ） 年级 人数 高一 550 高二 500 高三 450 合计 1500 A.18 B.22 C.40 D.60 4.已知某圆锥的底面半径为1，高为 ，则它的侧面积与底面积之比为（ ） A. B.1 C.2 D.4 5.平面向量 与 相互垂直，已知 ，且 与向量 的夹角是钝角，则 （ ） A. B. C. D. 6.已知点 为椭圆 的三个顶点，若 是正三角形，则 的离心率是（ ） A. B. C. D. 7.在 中，若 分别是方程 的两个根，则 （ ） A. B. C. D. 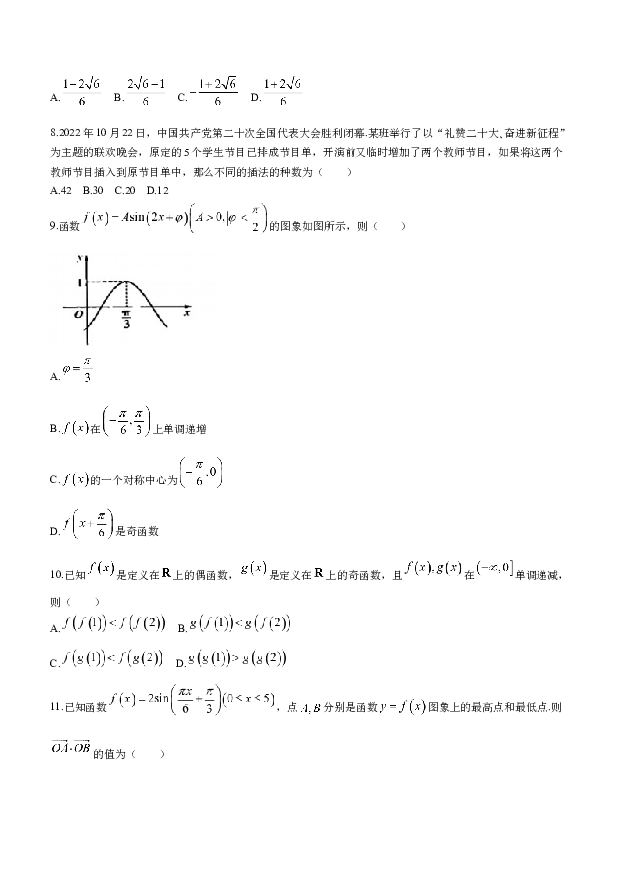8.2022年10月22日，中国共产党第二十次全国代表大会胜利闭幕.某班举行了以“礼赞二十大 ､奋进新 征程”为主题的联欢晩会，原定的5个学生节目已排成节目单，开演前又临时增加了两个教师节目，如果将这两个教师节目插入到原节目单中，那么不同的插法的种数为（ ） A.42 B.30 C.20 D.12 9.函数 的图象如图所示，则（ ） A. B. 在 上单调递增 C. 的一个对称中心为 D. 是奇函数 10.已知 是定义在 上的偶函数， 是定义在 上的奇函数，且 在 单调递减，则（ ） A. B. C. D. 11.已知函数 ，点 分别是函数 图象上的最高点和最低点.则 的值为（ ） A. B.3 C. D.7 12.下图改编自李约瑟所著的《中国科学技术史》，用于说明元代数学家郭守敬在编制《授时历》时所做的天文计算.图中的 都是以 O 为圆心的圆弧， 是为计算所做的矩形，其中 分别在线段 上， .记 ， 则不成立的等式是（ ） A. B. C. D. 第II卷（共90分） 二 ､填空题 （本大题共4小题，每小题5分，共20分） 13.函数 的图象在 处的切线方程为__________. 14.已知长方体 的底面是边长为 的正方形，若 ，则该长方体的外接球的表面积为__________. 15.若 分别是抛物线 与圆 上的点，则 的最小值为__________. 16.已知函数 在区间 单调，其中 为正整数， ，且 .则 图像的一条对称轴__________. 三 ､解答题 ：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算 步骤 ） 17.（本小题满分12分） 如图，四边形 是圆柱底面的内接四边形， 是圆柱的底面直径， 是圆柱的母线， 是 与 的交点， . （1）记圆柱的体积为 ，四棱锥 的体积为 ，求 ； （2）设点 在线段 上， ，求二面角 的余弦值. 18.（本小题满分12分） 记数列 的前 项和为 ，且 . （1）求数列 的通项公式； （2）对任意 ，求数列 的前项和 . 19.（本小题满分12分） 一个池塘里的鱼的数目记为 ，从池塘里捞出200尾鱼，并给鱼作上标识，然后把鱼放回池塘里，过一小段时间后再从池塘里捞出500尾鱼， 表示捞出的500尾鱼中有标识的鱼的数目. （1）若 ，求 的数学期望； （2）已知捞出500尾鱼中15尾有标识，试给出 的估计值（以使得 最大的 的值作为 的估计值）. 20.（本小题满分12分） 设 为曲线 上两点， 与 的横坐标之和为4. （1）求直线 的斜率； （2）设 为曲线 上一点， 在 处的切线与直线 平行，且 ，求直线 的方程. 21.（本小题满分12分） 已知 . （1）当 时，求曲线 在点 处的切线方程； （2）当 且 时，证明：曲线 在 轴的上方. 请考生在第22 ､ 23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程（10分） 如图，在极坐标系 Ox 中， ，弧 所在圆的圆心分别是 ，曲线 是弧 ，曲线 是弧 ，曲线 是弧 . （1）分别写出 的极坐标方程； （2）曲线 由 构成，若点 在 上，且 ，求 的极坐标. 23.选修4-5：不等式选讲（10分） 已知 . （1）当 时，求不等式 的解集； （2）若 时不等式 成立，求 的取值范围. 2023届高三第十二次模考数学（理科） 参考答案 一 ､选择题 ： 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B A C D C B A B C B D 二 ､填空题 13. 14. 15. 16. 三 ､解答题 ： 17.解： （1）由题设得 .于是 所以 . （2）以 为坐标原点， 的方向为 轴正方向， 为単位长，建立如图所示的空间直角坐标系 . 由（1）和题设得 ，所以 ， . 设平面 的法向量 ， 则 即 可取 . 设平面 的法向量 ， 则 即 可取 . 所以 . 因此二面角 的余弦值为 . 18.（本小题满分12分） 解：（1）由题设可知 ，当 时， ，则 ， 所以数列 的通项公式 （2）由（1）知 ，则 ① . ② ① - ② 得 化简得 . 19.（本小题满分12分） 解：（1）根据题意服从超几何分布，由超几何期望计算公式知 （2）当 时， 当 时， 令 ，由 求 最大的 解得 则